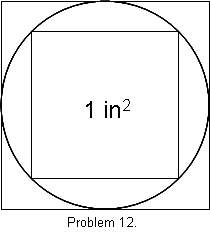
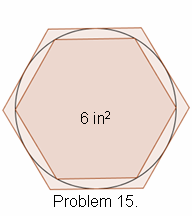
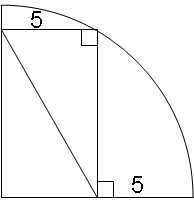
I noticed that the last 4 digits were palindromic, that is they read the same forwards as backwards. One mile later, the last 5 numbers were palindromic. One mile after that, the middle 4 out of 6 numbers were palindromic. And you ready for this? One mile later, all 6 were palindromic!The question is, what did I see on the odometer when he first looked? (1 Point)
22. The numbers 1-3 can easily be configured into a "difference triangle", an inverted triangle so that a lower number is the absolute difference between the two numbers above it. For example
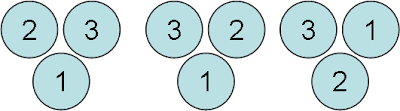 are all solutions. Find a three-row difference triangle for the numbers 1-6 using each number exactly once(1 Point), a four-row difference triangle with the numbers 1-10 using each number exactly once(2 Points), or a five-row difference triangle with the numbers 1-15 using each number exactly once (3 Points).
are all solutions. Find a three-row difference triangle for the numbers 1-6 using each number exactly once(1 Point), a four-row difference triangle with the numbers 1-10 using each number exactly once(2 Points), or a five-row difference triangle with the numbers 1-15 using each number exactly once (3 Points).23. Prove that there is no six-row difference triangle (defined in 22.) using the numbers 1-21 using each number exactly once. (5 Points)
24. Given a triangle, construct a triangle with twice the area using only a straight edge and compass. (1 Point)
25. A child is given the task of painting a box full of identical cubic wooden blocks with two colors – red and blue. Each face is to be either all blue or all red, never both blue and red on the same face. The blocks can be colored with all blue faces, all red faces or some combination of blue faces and red faces. How many different kinds of colored blocks the child can make? (1 Point)
Note: Two blocks are same if they can be put into matching positions by rotating. For example, all blocks with five red faces and one blue face are same.
26. A dart thrower hits any point on the dart board with equal probability. His dart board has an inner circle with half the radius of the whole board. What is the likelihood that he hits the inner circle in a single throw? (1 Point)
27. Construct a regular hexagon with only straight edge and a compass. A regular polygon is one with all edges the same length and all angles equal. (1 Point)
28. A golden rectangle is a rectangle whose proportions remain the same after removing the largest possible square with a single cut. Construct a golden rectangle with only a straight edge and compass. (2 Points)

29. Construct a regular pentagon with only a straight edge and a ru. (3 Points)
30. What is the value of x when
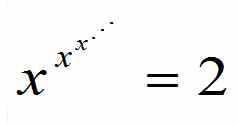
What is the value of x when
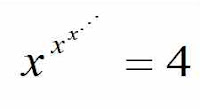
Explain the similarities or differences between the real value of x for the above two equations. (2 points)