Next 10

11. How many ways can you arrange 12 (1x2) dominoes into a 12x2 rectangle? (1 Point)

12. The area of the small square inscribed in the circle is one square inch. What is the area of the larger square? (2 Points)

13. How many ways can you make the sum of 11 using only the numbers 1 and 2? Count each ordering separately, that is
1 + 2 + 2 + 2 + 2 + 2 and
2 + 1 + 2 + 2 + 2 + 2 count as two ways. (1 Point)

14. There are three pairs of colored balls: two green, two red, and two blue. One ball from each pair is defective (weighs less). All three defective balls are of the same weight, so are the three perfect balls. Use two weighings on a simple balance scale to determine which balls are light and which are perfect (3 Point).

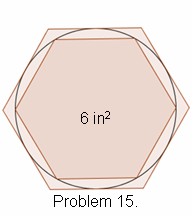
15. The area of the small hexagon inscribed in the circle is six square inches. What is the area of the larger hexagon? (2 Points)

16. Connect nine points arranged in a 3x3 square using 4 straight line segments without lifting your pencil or backtracking. Recall points have zero width they have been enlarged for clarity. (1 Point)

17. How many ways can you arrange five black billiard balls and five white billiard balls in a line? For instance "WWWWWBBBBB" is one such arrangement. All billiard balls must be used and spaces are not allowed. (2 Points)

18. How many combinations are there on a five button cypher-lock? On these locks you can press 1, 2, 3, 4, or 5 buttons at a time so long as each button is pressed at most once. For example pressing buttons 1 and 2 simultaneously followed by 4 and 5 simultaneously is a valid combination, whereas pressing buttons 1 and 2 followed by 2 and 3 is not. (3 points)

19. Solve the Rubik's Cube without help. (6 points)

20. A certain species of amoeba splits every minute. An hour after a pair of amoeba are put into the jar, the jar is full of amoeba. How long does it take for a single amoeba to fill the jar? (1 Point)